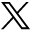Abstract
Purpose A method for measuring spinal curvature that provides a useful analog to the Cobb angle and is tolerant of degraded image quality is proposed. Conventional methods require a higher standard of discernibility for vertebra features and suffer high variability.
Methods Assumption is made that the natural representation of the spine for the purpose of scoliosis monitoring is that of a continuous curved contour rather than a series of discrete vertebral bodies with individual orientations. The angle that a tangent line to this contour makes with the vertical, expressed as a continuous function of height, is proposed as a metric for characterization of the curve. The Cobb angle can be approximated as the difference between the extrema of this function, and details of the function shape can provide additional markers for tracking curve variation and evolution. A method for deriving the angle function from coronal images of the spine is proposed, and both manual and automatic variants of the procedure are described.
Results The method is applied to conventional coronal radiographs and to magnetic resonance (MR) coronal views derived from volumetric acquisitions of the spine. Included in the latter category is an image exhibiting poor discrimination of vertebra features due to motion artifacts. The method permits extraction of the curve and Cobb angles in all cases.
Conclusions Because the spine contour is discernible even in low quality images where vertebral endplates may be obscured or poorly contrasted from surrounding tissue, the approach offers improved reliability, applicability across imaging modalities, and, in the case of x-rays, the possibility of a reduced radiation dose. Moreover, since it relies on larger image features and exploits the continuity of the spine, the contour-based approach is expected to reduce the variability associated with Cobb angle measurement.
Introduction
This paper seeks to advance a variation on the widely practiced manual methods of Cobb1 and Ferguson,2 and recently proposed digital approaches3-7 for characterizing spinal deformity in coronal images of the spine. These methods share a common trait: they rely on discernment, either by human visual identification or through computer enhancement, of the boundaries of individual vertebrae of the spine. The manual methods of Cobb and Ferguson, respectively, target the endplate surfaces and vertebra centers, and from these vertebra-specific features, infer characteristic angles for the curvature. Zhang et al.,3 Anitha and Prabhu,4 Abuzaghleh and Barkana,5 and Kundu et al.6 describe computer-aided approaches for isolating the vertebra features and computing angles, but all hinge on the application of Hough transform7 and edge detection for defining the vertebra boundaries. Dewaele8 measures curvature by deriving a geometric mapping to a normal reference spine image, but also relies on pre-processing to isolate the vertebra as closed shapes.
In their discussion of the crucial and increasing role of imaging in the diagnosis and management of scoliosis, Cassar-Pullicino and Eisenstein9 note that practitioners must balance the need for information that can guide effective treatment decisions against the radiation burden on the patient. Recent application of MR imaging to scoliosis evaluation (Schmitz et al.10) brings the advantage of eliminating the radiation exposure, but presents the dilemma of increased cost due to the time and resources involved.
What drives radiation burden, in the case of x-rays and scan time, in the case of MRI, is the quest for high quality images having clearly distinguishable vertebrae with sharp edge features. Relaxing the requirement on visibility of these features while still enabling the curvature measurement would have a universally positive effect, either reducing the x-ray radiation dose or the MRI scan time and cost.
Toward that end, this paper advocates a change to the fundamental mathematical model assumed by traditional methods. The variation proposed here centers on an abstract representation of the spine as a continuous curved contour with continuous derivatives, rather than a series of discrete vertebral bodies with individual angular inclinations. Rather than characterize curvature by means of the angular characteristics of selected vertebrae, it is proposed that the deformity be characterized in terms of geometric features gleaned from the overall structural curve.
The overall structural curvature of the spine is arguably the more natural focus for scoliosis monitoring, and the present day availability of digital imaging modalities as well as advancements in hardware and software for automated image processing makes such a focus immensely more practical than it would have been in decades past, when only manual methods and crude instruments were available for image analysis. It is asserted that a contour curvature-based methodology that relies less on the ability to visualize the individual vertebrae permits potentially significant benefits to both patient and practitioner, namely, reduced dependence on and lower dosing of x-rays, more flexibility in the choice of imaging method; and, through a focus on large rather than small image features, less measurement variability.
A New Angle
In discussing this approach, it is important to describe both what is being measured and how that measurement can be derived from available imagery. This section deals with the first of these two questions.
In general terms, scoliotic deformity manifests in deviation of the spine from its natural contour in both coronal and sagittal planes. Moreover, the vertebral bodies can independently exhibit rotations about their normal alignment in the contour. From a strictly mathematical perspective, the displacement of each vertebra from its normal state requires six dimensions to describe completely, accounting for all positional and rotational degrees of freedom. Compounding this, there are twenty-four such vertebrae to consider.
Accounting for all these degrees of freedom is impractical and arguably unnecessary, given the largely effective and almost universal application over many decades of the Cobb method, which reduces all these degrees of freedom to a single, or at most two, angles. The Cobb angle, introduced as a means to characterize curvature observed in coronal plane radiographs, is based on measurement of the orientation of opposing, maximally tilted endplates. When the process is complete, the at most two derived angles are used as a surrogate for the entire state of the spine.
Along with Cobb angle, Vrtovec et al.11overview a number of alternative characterizations of coronal spinal curvature, including Ferguson method,2 Greenspan index,12 Diab et al. method13 and Centroid method.14 These methods all rely on extraction of image features from individual vertebrae, predominately the vertebra centers, followed by reduction to a single discrete index.
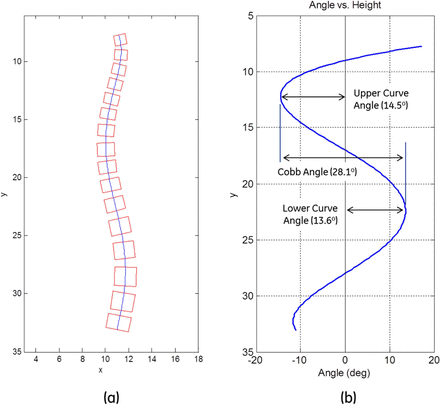
This paper proposes the characterization illustrated in Figure 1. Contour C in Figure 1a defines the composite structural curve (hereinafter, CSC) of the spine as projected onto the coronal plane. A tangent line to this contour makes an angle to the vertical that varies as a continuous function of height along the spine, yielding the characteristic angle function shown in Figure 1b. The normal non-scoliotic spine has an angle function that is zero at all heights; a scoliotic spine will exhibit a deviation from zero in one or more regions, with greater deviation corresponding to greater distortion of the spine.
Composite structural curve and corresponding angle function.
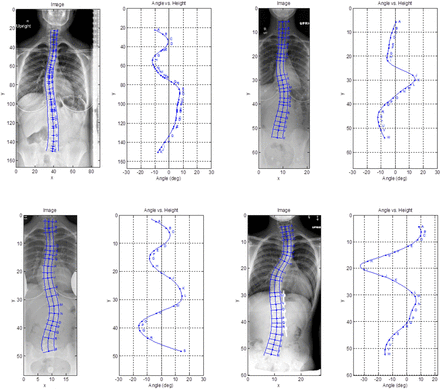
Figure 2 shows four example spine images and their corresponding angle functions. Magnitudes of distortion from the normal state are marked by displacement of the angle function from the reference line at zero degrees. Angle functions can exhibit either one or a multiplicity of distortion peaks, corresponding to the presence of thoracic, lumbar and more complex curvature states.
Sample scoliotic curves and corresponding angle functions.
Relationship to Cobb Angle
If the superior and inferior surfaces of the vertebrae are normal to the composite structural curve of the spine, then Cobb angles may be inferred from the peaks of the angle function, as shown in Figure 3. Single Cobb angles relate to the total displacement between the extrema (i.e., maxima and minima) of the angle function. Discrimination of upper and lower curves is accomplished by citing the magnitudes of the individual extrema.
Inferring critical angles from the angle function (idealized conditions).
Other authors (Stokes et al.,15 Berthonnaud and Dimnet, 16 Verre et al.,17 Tenaka,18 as examples) model the spine as a curved line and note the relationship to Cobb angle. The relationship is commonly expressed as the angular difference between normals to the curve at the points of inflection. This is mathematically equivalent to the absolute difference between the maximum and minimum value of the angle function. However, explicit consideration of the angle function, and its complete shape, makes the inflection points easier to discern, and can more readily reveal complex structural features.
There are two conditions that would result in a theoretical deviation between Cobb angles inferred in this manner (using either CSC or the equivalent angle function) and those obtained by the conventional technique. First, it is possible that the inflection points (angle function extrema) occur at locations between the vertebra surfaces. Second, it is possible for the vertebra surfaces not to be perpendicular to the CSC.
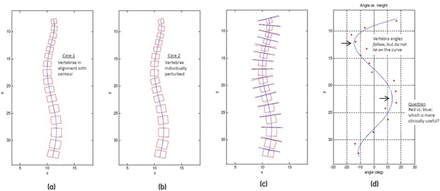
To see this, consider the schematic spine representations in Figure 4. The images in Figure 4a and Figure 4b show two spines that are equal in terms of their CSC. In 4a, all vertebrae are aligned normally (perpendicular) to the CSC. In 4b, the individual vertebrae exhibit small rotations about their normal alignments. Figure 4c shows the surface angles for the two cases, with blue lines corresponding to aligned vertebrae and red lines corresponding to non-aligned vertebrae. In the angle function plot of Figure 4d, the surface angles for the non-aligned vertebrae result in the red dots shown surrounding the angle curve, while the surface angles for the aligned vertebrae are subsumed by the blue angle curve itself. In this scenario, a Cobb angle measurement based on the conventional surface-based method would effectively entail comparing the red dots closest to the inflection points (extrema locations) indicated by the arrows. This measurement is clearly impacted by small vertebra rotations that do not manifest in a change to the overall structural curvature, while a measurement based on comparing the angle curve extrema would not be influenced. Note also that even if no such rotations were present (i.e., if all red dots were to lie on the blue curve), the possibility exists that the angle curve peak occurs between available surface measurements. In this case, limiting consideration to the vertebra surfaces would result in a miss of the lower inflection point, leading again to a difference (though here this latter influence is small) in the Cobb angle results from the two methods.
Comparison to conventional Cobb angle measurement.
The central thesis of this paper is that inferring the angle function as a vehicle for extracting Cobb angles, or as a method in its own right, for monitoring the progression of spinal curvature has inherent advantages over conventional surface-based Cobb angle or vertebra feature methods. The advantages stem from a reduced sensitivity to the as-imaged morphology of individual vertebrae and to imaging artifacts that impact the ability to discern exact surface angles, both key contributors to high variability of conventionally derived Cobb angles. As seen above, a Cobb angle equivalent can be extracted from the angle function. It should be clear that progression of the spinal curve will be evidenced by progressively larger excursions of the angle function, and correspondingly increasing Cobb angle equivalents. Because it is influenced by larger image features rather than highly localized features, the angle function is inherently more stable, in a statistical sense, than surface angles. As patients are monitored over time, provided that image quality is sufficient to infer the angle function (a lower standard than that required to visualize individual vertebra surfaces), it is expected that the corresponding Cobb angle trend will be smoother and exhibit lower measurement variability than that obtained conventionally.
Making the Measurement
With the measurement objective defined, the question of how to infer it from coronal images of the spine is now addressed. Simply stated, the angle function is derived by first extracting the composite structural curve (CSC) and then computing the tangent angle along the length of the curve. Since the angle function follows straightforwardly from the CSC, the focus here is on the details of the CSC extraction itself.
Extracting the CSC
It is useful to think of the CSC as a smooth contour that bisects the superior and inferior surfaces of all vertebrae and runs through all the vertebra centers, as illustrated in Figure 4a. In ideal terms, it is a locus of points that includes the midpoints of all upper and lower surfaces and the center points of all vertebrae, a collection that may be termed critical points of the spine image. However, due to imperfections in the anatomical symmetry of the vertebrae, as well as noise and artifacts of the imaging process, it is not always possible to adhere to both a smoothness property and a requirement of exact intersection of these critical points. Where these properties conflict, greater emphasis should be placed on smoothness, while tolerating small deviations of targeted critical points from the CSC.
The reason for the emphasis on smoothness is to promote statistical stability of the measurement. Stability confers a diminished influence of noise and artifacts on the measurement, and a reduced expectation of intra-observer and intra-image variation.
The method proposed for extracting a stable approximation of the CSC, and the defining aspect of the new approach, is to first isolate smooth contours defining the left and right edges of the vertebrae. These contours are modeled as parametric functions of height in the image. The mean of the two functions at each height then yields a smooth approximation of the CSC.
In more precise terms, the steps in the procedure are as follows, with implementation accomplished in custom software built on the MATLAB (MATLAB and Image Processing Toolbox Release 2012b, The MathWorks, Inc., Natick, MA, USA) computing and image processing platform:
From a coronal image of the spine, define a series of marker points such that the left edge contour of the spine is well represented,
Derive a parametric fit to the points, e.g., the coefficients of a low-order polynomial exhibiting minimum mean-square error to the defined points,
Evaluate the resulting parametric function over the vertical span of the defined points, to yield a smooth left-hand curve.
Repeat the process with right-edge points to yield a smooth right-hand curve,
Average the two curves at each vertical coordinate to yield a smooth CSC.
Note that Step 2 calls for a parametric fit, which need not intersect all marker points, as opposed to an interpolation, smooth or otherwise, that would necessarily intersect the defined points. In Figure 5, the plot at left shows one possible selection of points marking the left edge contour of a notional spine. The plot at right shows these points along with the polynomial described by
x = a5y5 + a4y4 + a3y3 + a2y2 + a1y + a0,
where the coefficients a0 thru a5 , computed using the MATLAB implementation of a standard leastsquares polynomial fitting algorithm, are chosen to minimize the error between the points and their projections on the resulting polynomial curve. (It is noted that smooth parametric curve representations other than polynomials are possible and can yield equivalent results, but the basic concept of a loworder representation of the edge curve remains the same. Within the choice of polynomials, order 5 is judged to offer an optimal balance between fit quality and smoothness, and is demonstrated in the examples of Figure 1 and Figure 2.)
Parametric curve fit to a set of left-edge points.
It is not necessary that edge points be defined for all vertebrae, rather, only a sufficient number to be representative of the spine contour. The tolerance of the curve fitting process to small positioning errors in the marker points implies that latitude exists in the selection of these points. This has the theoretical effect of reducing the variation that would result from different users applying their own discretion in marking the edge contour.
As seen, the critical and most difficult step in the above procedure is the extraction of representative, though not necessarily unique, left and right-edge marker points. When image quality is poor, this step is best accomplished manually. For higher quality images, wherein the spine is easily discerned from the surrounding anatomy, image processing techniques can be employed to automate the process.
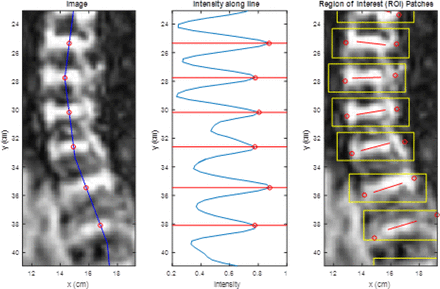
As an example, automation has been successfully applied to coronal MR images, which highlight the intervertebral discs in strong contrast to the vertebrae and surrounding soft tissue. The steps are as follows: a) using a mouse or other pointing device, a user draws a coarse path through the vertebrae from top to bottom; b) image intensity along this line is extracted, and the peaks are located; c) small sections of the image surrounding each peak, denoted region-of-interest (ROI) patches, are extracted; and d) spine edges are detected within each extracted ROI patch.
In Figure 6, the blue line in the left-hand image is the line drawn with the pointing device; the middle plot shows the image intensity along the line and corresponding detected peaks, which are mapped back to the image to yield the approximate centers of regions of interest. The right-hand image shows the automatically extracted ROI patches and detected spine edge points.
Automatic extraction of spine features.
The endpoint-finding algorithm described by Bonanni and DeBedout19 has been found effective in accomplishing step (d). The algorithm is suited to detecting the endpoints of short and arbitrarily oriented linesegment features such as laser lines. Each ROI patch detected in Figure 6 contains the MR rendering of a single intervertebral disc, which in a broad sense may be regarded as short and linear in character.
The ROI patch of Figure 7 is one such image extracted from the larger MR image of the spine using steps (a) thru (c), and the annotations indicate endpointfinding results from step (d). The red line defines the orientation of the disc, and is computed using a Radon transform.20,21 The red dots define the disc edges, and are computed by detecting where the image intensity along the line (and, for better noise immunity, averaged in the direction normal to the line) falls below a threshold.
Left and right edge detection from MR image of an intervertebral disc.
The level of edge-detection automation that is possible without compromising accuracy of the result, and the nature of applicable image processing edge detection techniques, are modality and image quality dependent. In low contrast or noisy images, automated processes are prone to errors and more user input is required. In the fallback, full manual case, the user visually inspects the image to discern the spine boundaries, then clicks and edits points for the defining left and right curves using a mouse.
However, even when image quality is poor, the spine edge contours are decidedly easier to identify visually than the orientation of the vertebra surfaces, because the curve contours are reinforced by the continuity of the spine. The CSC is defined by large image features; the vertebra surfaces by short features, making the CSC less subject to noise, low contrast, and other image distortions. This is the key advantage of the contour-based method, as further evidenced by examples in the next section.
Examples
The method of this paper is applicable across imaging modalities, and requires only that the contour of the spine, as opposed to the vertebra surfaces, be discernible in the image. In Figure 2, the method was applied to x-ray images. Extracted CSC curves for each of four patients highlight a common S-shaped distortion; derived angle functions provide a means to infer corresponding Cobb angles, and thus degree of severity. However, in addition to Cobb angles, the angle functions for these patients reveal highly specific features that distinguish the curves for each patient. It is believed that tracking these features, in addition to the Cobb values, may enhance the ability to detect changes in curvature over time.
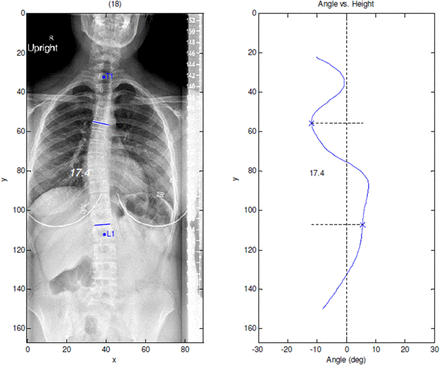
Figure 8 shows another x-ray example, this time with CSC contours excluded for clarity. Superimposed on the image are reference lines indicating the spinal levels selected by a trained practitioner for the purpose of assessing the Cobb angle. These levels are marked in the angle function graph by horizontal dashed lines. Examination of the angle function reveals that the lower level, selected on the basis of apparent surface angle, does not correspond to the location with maximum distortion based on contour curvature.
X-ray image example.
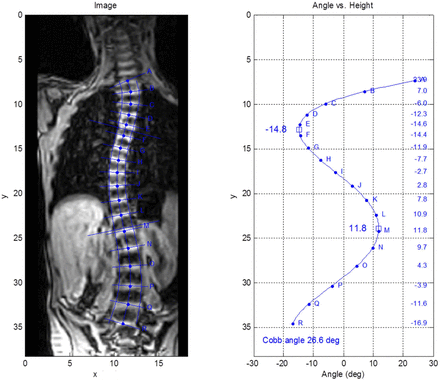
Figure 9 shows the method applied to an MR image, which accentuates soft tissue rather than bone. Note that although the disc surfaces are rendered less sharp than vertebra surfaces in the previous x-ray examples, this does not impede the ability to discern the spine contour; and thus, apply a contour-based method.
MR image example.
Perhaps the most compelling case for contour-based analysis is the possibility that it may be employed on low-dose x-rays or fast-scan MR images, or in other instances where image quality is compromised. Depending on the modality employed, the images may suffer from brightness variation and lack of dynamic range, or exhibit noise and motion artifacts. The vertebra endplates in these instances are often difficult or impossible to discern conclusively, rendering traditional methods useless.
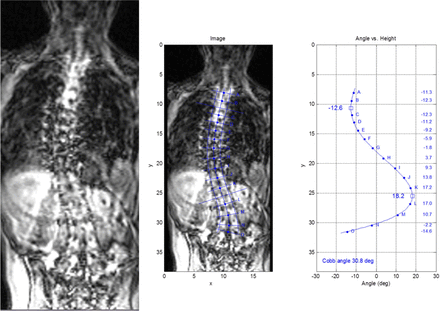
As an example, Figure 10 shows a spine image corrupted by motion artifacts that severely obscure the vertebra-disc interfaces. Despite this, it is still possible to discern the spine contour, and manually construct the CSC. The angle function resulting from the CSC reveals the Cobb angle.
Curvature measurement from a spine image with motion artifacts.
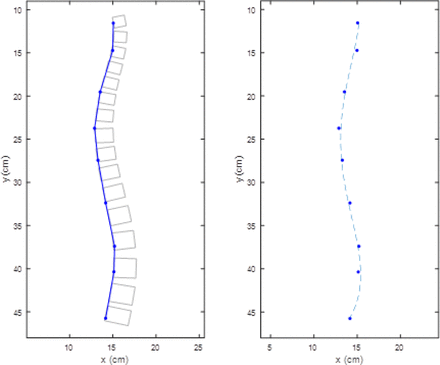
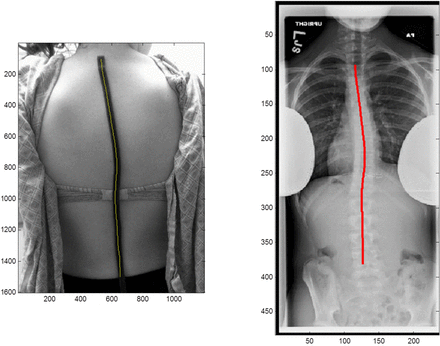
In the example of Figure 11, photography is employed as an alternative to invasive imaging. An adhesive foam strip was applied to the back of a scoliotic patient. Palpation of the back was performed, and the strip positioned to indicate the spine. An x-ray of the same patient is displayed alongside for comparison.
Spine CSC contour derived from a photographic image.
In this instance the CSC was extracted from the photographic image by isolating the foam strip and computing its centerline. At the right, the derived CSC is superimposed on the x-ray image. The result shows good agreement with the spine contour. This example illustrates that the CSC, and by extension, Cobb angle estimates may be possible without x-ray, MRI, or other invasive imaging procedures.
As a further extension, it is also possible to imagine that the adhesive strip might be instrumented with sensors and a computer that would perform the contour-based analysis directly and in real time; thus, eliminating even the need for acquiring and processing the photographic image.
Validation and Further Work
This paper has set out the details of a methodology. Critical questions remain regarding accuracy and reproducibility, as well as suitability of the method in a clinical setting. A first step toward validation the method is undertaken by Papaliodis et al.22 who report on a statistical comparison against independent evaluations by four trained orthopedic spine surgeons employing the conventional Cobb method. In that study of 58 diagnosed scoliosis patients, the method performed to within 5 degrees of the clinician average, with a standard deviation of 3.2 degrees. Further work to evaluate performance for lowdose x-rays, and trending over the course of patient treatment is planned.
Conclusions
A contour and angle-function based methodology is proposed as an alternative to the traditional vertebra endplate method for inferring Cobb angles. Contours are derived from marker points on the left and right edges of the spine, and averaged to form a single contour representation. Critical angles are computed from a derived angle function, rather than the vertebra-disc interfaces. Explicit discernment of vertebra outlines and feature analysis on individual vertebrae are not required. The method has the potential to be applied across imaging modalities, though further study is required to demonstrate insensitivity of the obtained result to the modality employed. Because of its reliance on larger image features, less refined image information is required, and there is less sensitivity to noise and image artifacts.
This methodology is proposed in hopes of benefiting both the patient, by reducing the need or the dosage requirement for x-rays, and the medical practitioner, by providing a more reliable and flexible means of monitoring the progress of scoliosis.
Acknowledgements
The author would like to acknowledge Dr. Allen Carl and Dr. Dean Papaliodis of Albany Medical College, and Dr. Lawrence Minkoff of Capital Region Upright MRI, for valuable discussions on scoliosis monitoring and treatment, and for providing sample imagery.
Disclosures & COI
The author declares no relevant financial disclosures or conflicts of interest.
- Copyright © 2017 ISASS - This manuscript is generously published free of charge by ISASS, the International Society for the Advancement of Spine Surgery